【問題】正12面体は何本の辺をきると展開図を書くことができますか。
また具体的な展開図を一つ書いてください。 2019 年栄光学園中入試問題改題
【ヒント】正12面体は正五角形が12枚でできています。
面の数は 12枚ですね。
それでは、辺の数は? 正五角形1つあたり5本の辺があります。
それが12枚あるので 5×12=60本の辺があります。
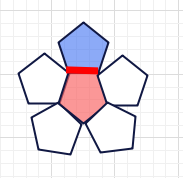
しかし、下の図のように、1つの辺を2面で共有してますので、
60÷2=30本となります。
正多面体の辺の数は 面の辺の数 × 面の数 ÷2となります。
2は1辺が共有する面の数は常に2面なためです。
それでは頂点の数はどうでしょうか。
公式を覚えるのではなく、上の「考え方」が頭に入っていればわかります。
1つの面の頂点の数は、5個です。
これが12面ありますので、12×5=60個となります。
1つの頂点を3面で共有してますので、60÷3=20個ですね。
頂点の数は 面の頂点の数 × 面の数÷(1点が共有する面の数) となります。
【解答】
正12面体の辺の数は
5(正五角形の辺の数)×12(正五角形の枚数)÷2(共有部分)=30本
となります。
また、12枚の面が辺どうしでつながっている必要がありますので、
11本の共有の辺でつながっている必要があります。
よって切る必要のある辺は、全体30-11=19本・・・(答え)
これを参考に具体的な展開図を4つほどご紹介します。(ほかにもあります)
代表的なものは、上の2つです。とくに1つ目はフォルム(形)がきれいですね。
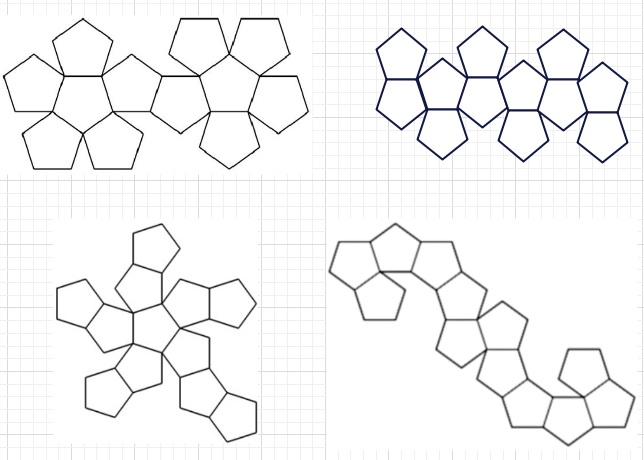
正12面体の展開図の数は 43380種類あるそうです。
どうやって計算するかわかりません(笑)が、今回の問題はそれを考える
入り口となる問題です。
これだけの種類あれば正5角形を12個
つなげると、ほぼ正12面体になりそうですね(笑)
コメント